Posts tagged "programming":

inline snippets and grouping in consult-recoll

I've just released a new version of consult-recoll, which implements a couple of features that i am really liking, namely, grouping of search results by mime type:

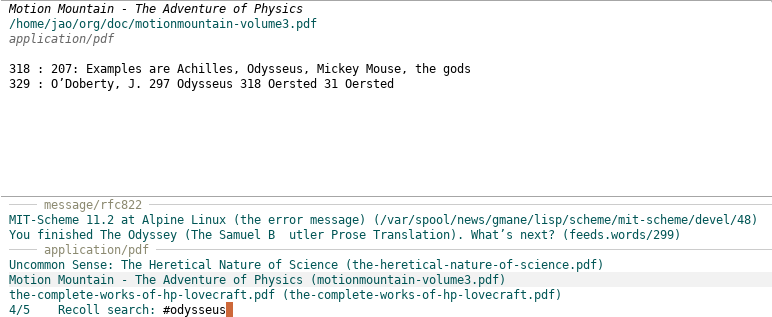
and inline snippets:

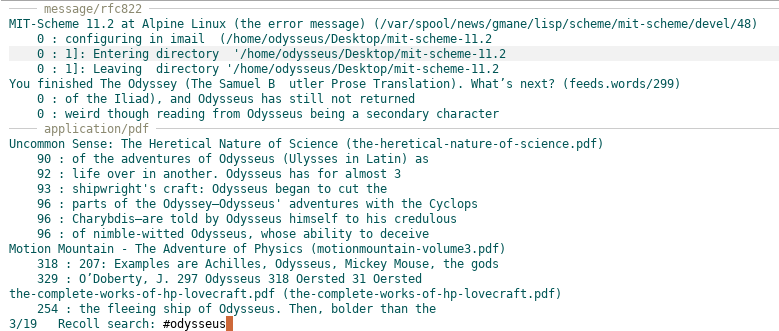
Happy searches!

the last straw: xmobar at codeberg

I've been thinking of moving xmobar's repository and issue tracker out from Github for a long time, for many reasons; but i had been procrastinating on it for the exact same amount of time. Until just now. The codepilot attack has finally broken the proverbial camel back, for reasons better explained in the Give up campaign site from the Software Freedom Conservancy.

There are some inconveniences associated with the move, like not being able to fully participate in issue discussion threads by email, or setting up CI tests, but i'm confident they'll be fixed in time, and, at any rate, the ultimate goal is worth putting up with them for as long as it takes.

So, please follow us to the new xmobar home over at Codeberg!

let's talk lisp

I just got a second-hand copy of this classic. Sometimes, used books are more charming than new ones:

fun with dependent types

reading source code is fun

From a recent checkout of the Emacs source code:

;;; desktop.el --- save partial status of Emacs when killed -*- lexical-binding: t -*-

;; Copyright (C) 1993-1995, 1997, 2000-2021 Free Software Foundation,
;; Inc.

;; Author: Morten Welinder <terra@diku.dk>
;; Keywords: convenience
;; Favorite-brand-of-beer: None, I hate beer.

;; This file is part of GNU Emacs.

Mine is Guinness :)

what's not to like

I've just discovered Codeberg, a code hosting site that, finally, has let me create a user with plain emacs-w3m, shows me content reasonably well there, with a refreshingly uncluttered layout, handles graciously org files (why, it's even generating a table of contents for me), has a good privacy policy, it's not under the wings of any corporation and had my preferred username free for grabs.

two decades of gnu mdk

I've just published GNU MDK 1.3.0, its 28th release, which finally migrates MDK's graphical user interface to GTK+ 3, to keep up with the, ahem, not-so-modern times and see to it that MDK keeps alive for at least another decade or two.

xmobar: a battery trick

i've been maintaining xmobar for more than a decade now, and i still use it daily and tweak it almost as often. With more than a hundred contributors besides myself, and many bugs to solve, i am always learning new things. The latest one, that font awesome thing everyone seems so fond of.

unlearn

For years, i've been using C-x p, C-x o and C-c <n> to move to other windows, but with ace window i am substituting all of them with M-o. Problem is, muscle memory interferes and i find myself clumsily moving around (and often lost) with the former ones. Or i did, before i followed an advice from Stefan Monnier in emacs-devel: unbind those keys you want to forget, and you'll get an error when you relapse.

imagine

Posted to comp.lang.scheme on January 17, 1996, for Scheme's twentieth birthday.

literate programming

I got started with literate programming many years ago, out of admiration for almost everything else i knew done by Donal Knuth, and tried my hand at it in some toyish projects in OCaml and Scheme. So it wasn't without lack of enthusiasm that i plunged into the literate world.

donald stewart on haskell in the large

Last October Don Stewart gave a very interesting talk at CodeNode on his experience using Haskell at a large scale. And by large, he means millions of lines of code. Although he wasn't allowed to talk about the very specifics of the code, his talk is full of interesting remarks that i found resonate with my experience. They actually convinced me that the next language i should try in production should be OCaml.

spj's y-combinator in scheme

Recently i bought a second-hand copy of Simon Peyton Jones' classic The implementation of functional programming languages, and i've been having some very pleasant reading hours during the last week.

where my mouth is

For many years, i've been convinced that programming needs to move forward and abandon the Algol family of languages that, still today, dampens the field. And that that forward direction has been signalled for decades by (mostly) functional, possibly dynamic languages with an immersive environment. But it wasn't until recently that i was able to finally put my money where my mouth has been all these years.

enjoying haskell

I've been reading about Haskell quite a bit during the last months, writing some actual code, and liking the language more and more. After many years favouring dynamically typed languages, i'm beginning to really appreciate Haskell's type system and the benefits it brings to the table.

erlang now!

I don't know whether Monty Python ever wrote a gag on programming languages, but if they did, this Erlang video must be it. The funniest thing is that it is pretty serious, and does a great job showing one of my most cherished abilities when using dynamic languages, namely, adding new functionality to a running system on the fly. As for the Monty Python bit, well, you have to see the to know what i mean: i kept laughing out loud during most of its twelve minutes (those Ericsson engineers seem to be taken from The Larch, but then maybe it's just my sense of humor).

playing with eli's toys

Some weeks ago, as a way to give a serious try to the PLT environment, i wrote my first (and only so far) PLT package, MzFAM, a File Alteration Monitor for MzScheme. MzFAM consists of a set of PLT-scheme modules providing utilities to monitor and react to filesystem changes. It exports a high-level interface consisting of monitoring tasks that run as independent threads and invoke callback procedures each time a file alteration is detected. These high-level tasks are implemented using either Linux's FAM/Gamin monitors or, in systems where it is not available, a pure Scheme fall-back implementation. (A native implementation for BSD systems, based on the kevent/kqueue system calls (see also this nice article to learn more), is on the works.)

programmers go bananas

I learned programming backwards, plunging right on into C and, shortly after, C++ and Java from the very beginning. I was knee deep in complex data structures, pointers and abstruse template syntax in no time. And the more complex it all felt, the more i thought i was learning. Of course, i was clueless.

continuation kata

If you have a little Scheme under your belt, just plunge into the challenge right now:

beyond mainstream object-oriented programming

After a few scheming years, i had come to view objects as little more than poor-man closures. Rolling a simple (or not so simple) object system in scheme is almost a textbook exercise. Once you've got statically scoped, first-order procedures, you don't need no built-in objects. That said, it is not that object-oriented programming is not useful; at least in my case, i find myself often implementing applications in terms of a collection of procedures acting on requisite data structures. But, if we restrict ourselves to single-dispatch object oriented languages, i saw little reason to use any of them instead of my beloved Scheme.

as simple as possible...

Einstein's (attributed) quotation has become an aphorism, taken for granted by every mathematician or physicist i've ever met (to mention two kinds of people i've been frequently involved with). One would expect the same attitude from a community that invented the term 'no silver bullet', and yet, since i got into computer science, first for fun and later on for a living, i've found lots of people with, er, a different viewpoint. Take for instance this excerpt from Lisp is sin, a widely cited and commented article by Sriram Krisnan:

the joy of repl

Back in the old days i was a macho C++ programmer, one of those sneering at Java or any other language but C, willing to manage my memory and pointers and mystified by the complexity of the template syntax (it was difficult and cumbersome, ergo it had to be good). Everyone has a past.